阅读材料：对于任何实数，我们规定符号
的意义是=ad﹣bc．例如：
=1×4﹣2×3=﹣2，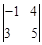
=（﹣2）×5﹣4×3=﹣22．
（1）按照这个规定，请你计算
的值；
（2）按照这个规定，请你计算：当x2﹣4x+4=0时，
的值．
相关试题
的值．
（2）
， 6 ，
，0，
，写出整数的和与分数的积的差
，
，
，
这六个数中，负数有m个，整数有n个，非负数有k个，求
的值。
，
， 0， -|-2︳， 2．5 |-3︳相关知识点
推荐套卷
阅读材料：对于任何实数，我们规定符号的意义是=ad﹣bc．例如：=1×4﹣2×3=﹣2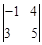，=（﹣2）×5﹣4×3=﹣22．
（1）按照这个规定，请你计算的值；
（2）按照这个规定，请你计算：当x2﹣4x+4=0时，的值．
粤公网安备 44130202000953号