已知，在矩形ABCD中，AB=4，BC=2，点M为边BC的中点，点P为边CD上的动点（点P异于C、D两点）。连接PM，过点P作PM的垂线与射线DA相交于点E（如图）。设CP=x，DE=y。
（1）写出y与x之间的函数关系式 ▲ ；
（2）若点E与点A重合，则x的值为 ▲ ；
（3）是否存在点P，使得点D关于直线PE的对称点D′落在边AB上？若存在，求x的值；若不存在，请说明理由。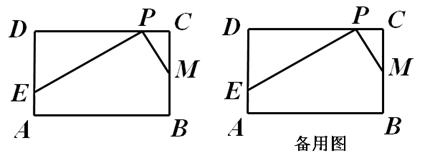
．
，试求A-B”时，把“A-B”看成了“A+B”，结果求出的答案是
，请你帮他求出“A-B”的正确答案．
，其中
，
．
，0，
，
，
．相关知识点
推荐套卷
已知，在矩形ABCD中，AB=4，BC=2，点M为边BC的中点，点P为边CD上的动点（点P异于C、D两点）。连接PM，过点P作PM的垂线与射线DA相交于点E（如图）。设CP=x，DE=y。
（1）写出y与x之间的函数关系式 ▲ ；
（2）若点E与点A重合，则x的值为 ▲ ；
（3）是否存在点P，使得点D关于直线PE的对称点D′落在边AB上？若存在，求x的值；若不存在，请说明理由。
粤公网安备 44130202000953号