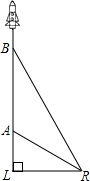如图，某种新型导弹从地面发射点Ｌ处发射，在初始竖直加速飞行阶段，导弹上升的高度y(km)与飞行时间x(s)之间的关系式为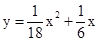
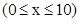．发射3 s后，导弹到达A点，此时位于与L同一水平面的R处雷达站测得AR的距离是2 km，再过3s后，导弹到达B点．
(1)(4分)求发射点L与雷达站R之间的距离；
(2)(4分)当导弹到达B点时，求雷达站测得的仰角(即∠BRL)的正切值．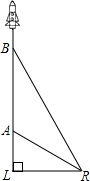
．
(0 ，5)和 点(–1 ，0)，且对称轴为
，求函数解析式.
,
，解这个直角三角形.相关知识点
推荐套卷
如图，某种新型导弹从地面发射点Ｌ处发射，在初始竖直加速飞行阶段，导弹上升的高度y(km)与飞行时间x(s)之间的关系式为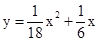 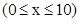．发射3 s后，导弹到达A点，此时位于与L同一水平面的R处雷达站测得AR的距离是2 km，再过3s后，导弹到达B点．
(1)(4分)求发射点L与雷达站R之间的距离；
(2)(4分)当导弹到达B点时，求雷达站测得的仰角(即∠BRL)的正切值．
粤公网安备 44130202000953号