已知椭圆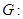
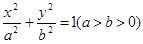 的离心率为
的离心率为 =
= ,椭圆
,椭圆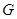 上的点
上的点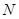 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆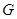 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点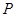 在椭圆上,且位于
在椭圆上,且位于 轴的上方,
轴的上方, .
.
(I) 求椭圆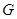 的方程;
的方程;
(II)求点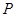 的坐标;
的坐标;
(III) 设 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点, 到直线AP的距离等于
到直线AP的距离等于 ,求椭圆上的点到点
,求椭圆上的点到点 的距离
的距离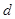 的最小值.
的最小值.
相关知识点
推荐套卷
已知椭圆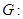
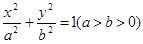 的离心率为
的离心率为 =
= ,椭圆
,椭圆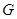 上的点
上的点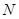 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆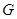 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点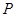 在椭圆上,且位于
在椭圆上,且位于 轴的上方,
轴的上方, .
.
(I) 求椭圆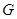 的方程;
的方程;
(II)求点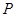 的坐标;
的坐标;
(III) 设 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点, 到直线AP的距离等于
到直线AP的距离等于 ,求椭圆上的点到点
,求椭圆上的点到点 的距离
的距离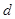 的最小值.
的最小值.