已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:当 取不等于l的实数时,此方程总有两个实数根.
取不等于l的实数时,此方程总有两个实数根.
(2)若 是此方程的两根,并且
是此方程的两根,并且 ,直线
,直线 :
: 交
交 轴于点A,交
轴于点A,交 轴于点B,坐标原点O关于直线
轴于点B,坐标原点O关于直线 的对称点O′在反比例函数
的对称点O′在反比例函数 的图象上,求反比例函数
的图象上,求反比例函数 的解析式.
的解析式.
(3)在(2)的成立的条件下,将直线 绕点A逆时针旋转角
绕点A逆时针旋转角 ,得到直线
,得到直线 ′,
′, ′交
′交 轴于点P,过点P作
轴于点P,过点P作 轴的平行线,与上述反比例函数
轴的平行线,与上述反比例函数 的图象交于点Q,当四边形APQO′的面积为
的图象交于点Q,当四边形APQO′的面积为 时,求角
时,求角 的值.
的值.
相关知识点
推荐套卷
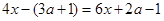 的解相同,求式子(2
的解相同,求式子(2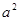 +3
+3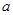 -4)-(-3
-4)-(-3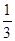 ∠β的值
∠β的值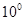 后等于这个角的余角的3倍,求这个角的度数.
后等于这个角的余角的3倍,求这个角的度数.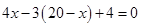
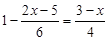
 .
.
 ,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形?若存在,请求出点P坐标;若不存在,请说明理由.
,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形?若存在,请求出点P坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号