如图,在直角坐标系中,点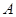 的坐标为
的坐标为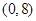 ,点
,点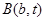 在直线
在直线 上运动,点
上运动,点 、
、 、
、 分别为
分别为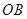 、
、 、
、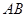 的中点,其中
的中点,其中 是大于零的常数.
是大于零的常数.
(1)请判断四边形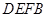 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)试求四边形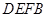 的面积
的面积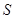 与
与 的关系式;
的关系式;
(3)设直线 与
与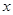 轴交于点
轴交于点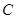 ,问:四边形
,问:四边形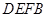 能不能是矩形?若能,求出
能不能是矩形?若能,求出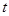 的值;若不能,说明理由.
的值;若不能,说明理由.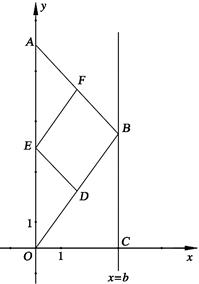
相关知识点
推荐套卷
如图,在直角坐标系中,点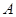 的坐标为
的坐标为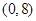 ,点
,点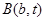 在直线
在直线 上运动,点
上运动,点 、
、 、
、 分别为
分别为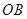 、
、 、
、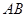 的中点,其中
的中点,其中 是大于零的常数.
是大于零的常数.
(1)请判断四边形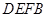 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)试求四边形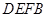 的面积
的面积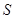 与
与 的关系式;
的关系式;
(3)设直线 与
与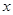 轴交于点
轴交于点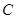 ,问:四边形
,问:四边形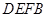 能不能是矩形?若能,求出
能不能是矩形?若能,求出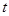 的值;若不能,说明理由.
的值;若不能,说明理由.