有A、B两个不透明的布袋,A袋中有两个完全相同的小球,分别标有数字0和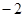 ;B袋中有三个完全相同的小球,分别标有数字
;B袋中有三个完全相同的小球,分别标有数字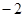 、0和1.小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
、0和1.小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
⑴写出点Q所有可能的坐标;
⑵求点Q在x上的概率;
⑶在平面直角坐标系xOy中,⊙O的半径是2,求过点Q能作⊙O切线的概率.
相关知识点
推荐套卷
有A、B两个不透明的布袋,A袋中有两个完全相同的小球,分别标有数字0和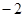 ;B袋中有三个完全相同的小球,分别标有数字
;B袋中有三个完全相同的小球,分别标有数字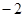 、0和1.小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
、0和1.小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
⑴写出点Q所有可能的坐标;
⑵求点Q在x上的概率;
⑶在平面直角坐标系xOy中,⊙O的半径是2,求过点Q能作⊙O切线的概率.