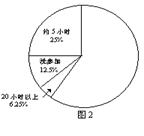
寒假期间，某校同学积极参加社区公益活动. 开学后，校团委随机选取部分学生对每人的“累计参与时间”进行了调查，将数据绘制成图1、图2. 请结合这两幅不完整的统计图解答下列问题：
（1）这次调查共选取了多少名学生？
（2）将图1的内容补充完整；
（3）求图2中“约15小时”对应的圆心角度数，并把图2的内容补充完整；
（4）若该校共有学生680人，估计这个寒假有多少学生参加了社区公益活动？
相关试题
（本小题12分）如图12，在Rt△ACB中，∠ACB＝90°，点O是AC边上的一点，以O为圆心，OC为半径的圆与AB相切于点D，连接OD．
（1）△ADO∽△ACB．
（2）若⊙O的半径为1，求证：AC＝AD·BC
（本小题12分）某学校对某班学生“五·一”小长假期间的度假情况进行调查，并根据收集的数据绘制了两幅不完整的统计图，请你根据图中提供的信息解答下面的问题：
（1）求出该班学生的总人数．
（2）补全频数分布直方图．
（3）求出扇形统计图中∠α的度数．
（4）你更喜欢哪一种度假方式．
（本小题10分）联通公司手机话费收费有A套餐（月租费15元，通话费每分钟0．1元）和B套餐（月租费0元，通话费每分钟0．15元）两种。设A套餐每月话费为y1（元），B套餐每月话费为y2（元），月通话时间为x分钟．
（1）分别表示出y1与x，y2与x的函数关系式．
（2）月通话时间为多长时，A、B两种套餐收费一样？
（3）什么情况下A套餐更省钱？
相关知识点
推荐套卷
粤公网安备 44130202000953号