如图，小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB＝1.2米，BP＝1.8米，PD＝12米，那么该古城墙的高度是__米．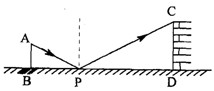
的平方根是 ．
相关知识点
推荐套卷
如图，小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB＝1.2米，BP＝1.8米，PD＝12米，那么该古城墙的高度是__米．
粤公网安备 44130202000953号