有下列4个命题：
①、函数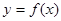
在一点的导数值为
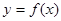是函数在这点取极值的充要条件；
②、若椭圆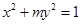
的离心率为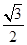
，则它的长半轴长为1；
③、对于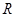
上可导的任意函数
，若满足
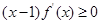，则必有
④、经过点（1,1）的直线，必与椭圆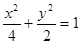
有2个不同的交点。其中真命题的为
将你认为是真命题的序号都填上）
，则
= 
的定义域为 
是奇函数，则实数
时的椭圆的标准方程是 .推荐套卷
有下列4个命题：
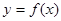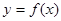①、函数在一点的导数值为是函数在这点取极值的充要条件；
②、若椭圆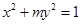的离心率为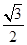，则它的长半轴长为1；
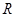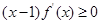③、对于上可导的任意函数，若满足，则必有
④、经过点（1,1）的直线，必与椭圆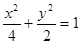有2个不同的交点。其中真命题的为
将你认为是真命题的序号都填上）
粤公网安备 44130202000953号