(本小题满分12分)某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
⑴ 若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
⑵ 若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
相关知识点
推荐套卷
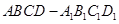 是正方体,其中
是正方体,其中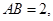


 ;
;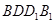 所成的锐二面角
所成的锐二面角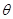 的余弦值;
的余弦值;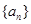 ,
, ,前
,前 项和为
项和为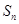 .各项均为正数的等比数列列
.各项均为正数的等比数列列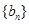 满足:
满足: ,
, ,且
,且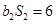 .
.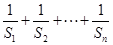
 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足

 的大小;
的大小; 的取值范围。
的取值范围。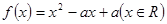 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式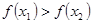 成立.
成立.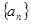 的前
的前 项和
项和 ,
, 中,令
中,令 ,
,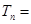
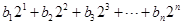 ,求
,求 ;
; 中,所有满足
中,所有满足 的正整数
的正整数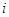 的个数称为这个数列
的个数称为这个数列 (
( ,它们在
,它们在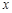 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.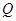 ,点
,点 都满足
都满足 ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号