在矩形ABCD中,AB=2,AD=3,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.
(1)连接AE,当△APE与△ADE全等时,求BP的长;
(2)若设BP为x,CE为y,试确定y与x的函数关系式.当x取何值时,y的值最大?最大值是多少?
(3)若PE∥BD,试求出此时BP的长.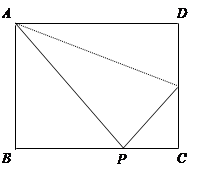
相关知识点
推荐套卷
在矩形ABCD中,AB=2,AD=3,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.
(1)连接AE,当△APE与△ADE全等时,求BP的长;
(2)若设BP为x,CE为y,试确定y与x的函数关系式.当x取何值时,y的值最大?最大值是多少?
(3)若PE∥BD,试求出此时BP的长.