温州市处于东南沿海，夏季经常遭受台风袭击，一次，温州气象局测得台风中心在温州市A的正西方向300千米的B处，以每小时10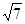
千米的速度向东偏南30°的BC方向移动，距台风中心200千米的范围是受台风严重影响的区域。试问：
（1）台风中心在移动过程中离温州市最近距离是多少千米?
（2）温州市A是否受台风影响？若不会受到，请说明理由；由，若会受到，求出温州市受台风严重影响的时间．
，求a、m、n的值。
；
；
的高
所在直线与高
所在直线相交于点F。
过点
作
交直线
于点
，求证：
（1）中的其他条件不变，则
之间满足怎样的数量关系？并给出证明。
相关知识点
推荐套卷
温州市处于东南沿海，夏季经常遭受台风袭击，一次，温州气象局测得台风中心在温州市A的正西方向300千米的B处，以每小时10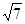千米的速度向东偏南30°的BC方向移动，距台风中心200千米的范围是受台风严重影响的区域。试问：
（1）台风中心在移动过程中离温州市最近距离是多少千米?
（2）温州市A是否受台风影响？若不会受到，请说明理由；由，若会受到，求出温州市受台风严重影响的时间．
粤公网安备 44130202000953号