意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，……，其中从第三个数起，每一个数都等于它前面两个数的和． 现以这组数中的各个数作为正方形的长度构造一组正方形（如下图），再分别依次从左到右取2个，3个，4个，5个正方形拼成如下长方形并记为①，②，③，④，相应长方形的周长如下表所示：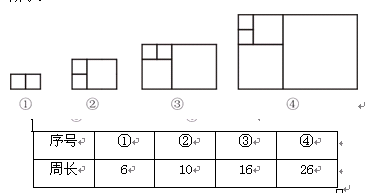
若按此规律继续作长方形，则序号为⑧的长方形周长是（ ）
| A．288 | B． 110 | C．128 | D．178 |
相关试题
将抛物线y=x2平移得到抛物线y=x2+3,则下列平移过程正确的是 ( )
| A．向上平移3个单位 | B．向下平移3个单位 |
| C．向左平移3个单位 | D．向右平移3个单位 |
下列说法正确的是 ( )
| A．掷两枚硬币，一枚正面朝上，一枚反面超上是不可能事件 |
| B．随意地翻到一本书的某页，这页的页码为奇数是随机事件 |
| C．经过某市一装有交通信号灯的路口，遇到红灯是必然事件 |
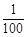D．某一抽奖活动中奖的概率为 ,买100张奖券一定会中奖 |
的图象如图所示，那么一次函数
与反比例函数
在同一坐标系内的图象大致为
，则图中阴影部分的面积为
相关知识点
推荐套卷
粤公网安备 44130202000953号