如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE，ED，DB组成，已知河底ED是水平的，ED＝16m，AE＝8m，抛物线的顶点C到ED的
距离是11m，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．
(1)求抛物线的解析式；
(2)已知从某时刻开始的40h内，水面与河底ED的距离h(单位：m)随时间t(单位：h)的变化满足函数
关系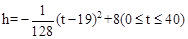
且当水面到顶点C的距离不大于5m时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？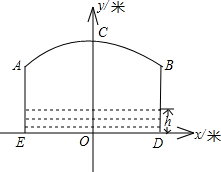
相关试题
超市、书店、玩具店依次坐落在一条东西走向的大街上，超市在书店西边20米处，玩具店位于书店东边50米处．小明从书店出来沿街向东走了50米，接着又向东走了-80米，此时小明的位置在何处？在数轴上标出超市、书店、玩具店的位置，以及小明最后的位置．
初一（4）班在一次联欢活动中，把全班分成5个队参加活动，游戏结束后，5个队的得分如下：
A队：-50分；B队：150分；C队：-300分；D队：0分；E队：100分．
（1）将5个队按由低分到高分的顺序排序；
（2）把每个队的得分标在数轴上，并将代表该队的字母标上；
（3）从数轴上看A队与B队相差多少分？C队与E队呢？
相关知识点
推荐套卷
粤公网安备 44130202000953号