定义 为函数
为函数 的“特征数”.如:函数
的“特征数”.如:函数 的“特征数”是
的“特征数”是 ,函数
,函数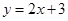 的“特征数”是
的“特征数”是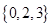 ,函数
,函数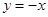 的“特征数”是
的“特征数”是

(1)将“特征数”是 的函数图象向下平移2个单位,得到一个新函数,这个新
的函数图象向下平移2个单位,得到一个新函数,这个新
函数的解析式是 ;
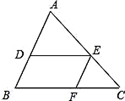
(2)在(1)中,平移前后的两个函数分别与 轴交于A、B两点,与直线
轴交于A、B两点,与直线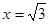 分别交于
分别交于
D、C两点,在给出的平面直角坐标系中画出图形,判断以A、B、C、D四点为顶点的四边形形状,并说明理由;
(3)若(2)中的四边形与“特征数”是的函数图象有交点,试求出实数
b 的取值范围.
相关知识点
推荐套卷


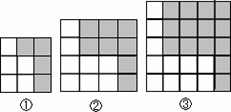
 ?如果存在,是第几个图形;如果不存在,请说明理由.
?如果存在,是第几个图形;如果不存在,请说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号