已知二次函数 在
在 和
和 时的函数值相等。
时的函数值相等。
(1)求二次函数的解析式;
(2)若一次函数 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A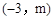 ,求m和k的值;
,求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移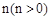 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线 向上平移n个单位。请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围。
向上平移n个单位。请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围。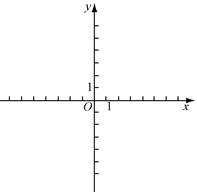
相关知识点
推荐套卷
已知二次函数 在
在 和
和 时的函数值相等。
时的函数值相等。
(1)求二次函数的解析式;
(2)若一次函数 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A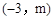 ,求m和k的值;
,求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移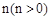 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线 向上平移n个单位。请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围。
向上平移n个单位。请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围。