（理）（1）证明不等式：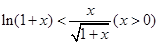
（2）已知函数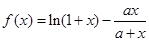
在
上单调递增，求实数
的取值范围.
（3）若关于x的不等式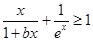
在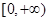
上恒成立，求实数
的最大值.
（文）已知函数
的导函数的图象关于直线x=2对称.
（Ⅰ）求b的值；
（Ⅱ）若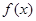
在
处取得极小值，记此极小值为
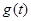，求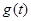的定义域和值域.
满足：对于
都有
求
（2）若
求
求
取哪些值时，无穷数列
满足性质：对于
且
求
求数列
的通项公式.
中，
；数列
中，
。当
时，
,
，求
,
.推荐套卷
（理）（1）证明不等式：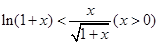
（2）已知函数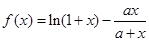在上单调递增，求实数的取值范围.
（3）若关于x的不等式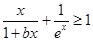在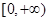上恒成立，求实数的最大值.
（文）已知函数的导函数的图象关于直线x=2对称.
（Ⅰ）求b的值；
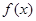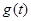（Ⅱ）若在处取得极小值，记此极小值为，求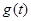的定义域和值域.
粤公网安备 44130202000953号