如图①,在Rt△ABC中,已知∠A=90°,AB=AC,G、F分别是AB、AC上的两点,且GF∥BC,AF=2,BG=4。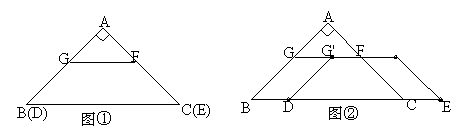
(1)求梯形BCFG的面积;
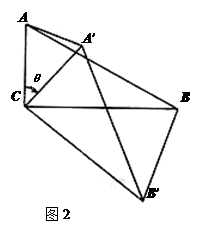
(2)有一梯形DEFG与梯形BCFG重合,固定△ABC,将梯形DEFG向右运动,直到点D与点C重合为止,如图②.
①若某时段运动后形成的四边形BDG'G中,DG⊥BG',求运动路程BD的长,并求此时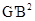 的值;
的值;
②设运动中BD的长度为x,试用含x的代数式表示出梯形DEFG与Rt△ABC重合部分的面积S。
相关知识点
推荐套卷

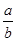
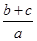

 轴、
轴、 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在 经过A、C两点,与
经过A、C两点,与 ,△ACQ的面积 S△ACQ=
,△ACQ的面积 S△ACQ= ,直接写出
,直接写出
 (0°<
(0°<


 粤公网安备 44130202000953号
粤公网安备 44130202000953号