一个盒子中装有4张形状大小都相同的卡片，卡片上的编号分别为1、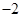
、
、
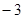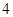，现从盒子中随机抽取一张卡片，将其编号记为
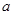，再从剩下的三张中任取一张，将其编号记为
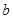，这样就确定了点
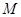的一个坐标，记为
．
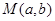（1）求第一次抽到编号为
的概率；
（2）请用树状图或列表法，求点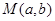在第四象限的概率.
相关试题
与x的
的和是非负数相关知识点
推荐套卷
一个盒子中装有4张形状大小都相同的卡片，卡片上的编号分别为1、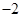、、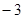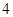，现从盒子中随机抽取一张卡片，将其编号记为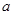，再从剩下的三张中任取一张，将其编号记为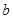，这样就确定了点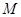的一个坐标，记为．
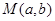（1）求第一次抽到编号为的概率；
（2）请用树状图或列表法，求点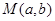在第四象限的概率.
粤公网安备 44130202000953号