为了更好地治理木兰溪水质，保护环境，市治污公司决定购买10台污水处理设备，现有A B两种设备，A B单价分别为a万元/台 b万元/台 月处理污水分别为240吨/月 200吨/月 ，经调查 买一台A型设备比买一台B型设备多2万元 ， 购买2台A型设备比购买3台B型设备少6万元。求a.、 b的值 。
经预算；市治污公司购买污水处理器的资金不超过105万元 ，你认为该公司有哪几种购买方案？
在（2）的条件下，若每月处理的污水不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的方案
相关试题
如图,△ABC中，∠C=90°，BC=8cm，
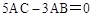，点P从B点出发，沿BC方向以2cm/m的速度移动，点Q从C出发，沿CA方向以1cm/m的速度移动。若P、Q同时分别从B、C出发，经过多少时间△CPQ与△CBA相似？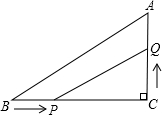
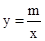如图，在平面直角坐标系中，双曲线
和直线y=kx+b交于A，B两点，点A的坐标为（﹣3，2），BC⊥y轴于点C，且OC=6BC．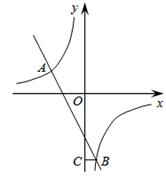
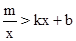（1）求双曲线和直线的解析式；
（2）直接写出不等式
的解集．
如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连结AC，CE.
（1）求证：∠B=∠D；
（2）若AB=4，BC-AC=2，求CE的长.
如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？
.
相关知识点
推荐套卷
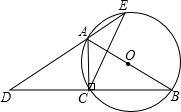
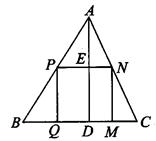
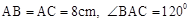粤公网安备 44130202000953号