如图①,△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A顺时针旋转,当DF边与AB边重合时,旋转中止,不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图②问:始终与△AGC相似的三角形有_______及_______
设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由)
问:当x为何值时,△AGH是等腰三角形?

相关知识点
推荐套卷
 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)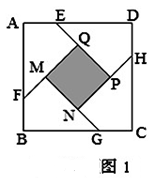

 ,则AD的长为__________.
,则AD的长为__________.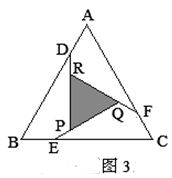
 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
 ,求BF的长.
,求BF的长.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号