如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线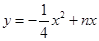 y=" -" 4x点D.直线OD的解析式为
y=" -" 4x点D.直线OD的解析式为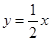 ,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.
,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.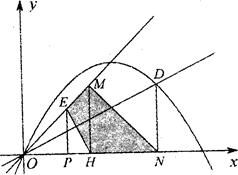
直接写出点D的坐标及n的值
判断抛物线的顶点是否在直线OM上?并说明理由
设以M、E、H、N为顶点的四边形的面积为S.当x≠3[时,求S与x的函数关系式.
相关知识点
推荐套卷
如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线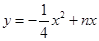 y=" -" 4x点D.直线OD的解析式为
y=" -" 4x点D.直线OD的解析式为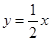 ,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.
,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.
直接写出点D的坐标及n的值
判断抛物线的顶点是否在直线OM上?并说明理由
设以M、E、H、N为顶点的四边形的面积为S.当x≠3[时,求S与x的函数关系式.