如图,直线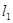 交直线
交直线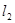 于
于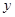 轴上一点
轴上一点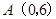 ,交
,交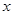 轴上另一点
轴上另一点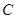 ,
,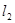 交
交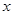 轴于另一点
轴于另一点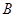 ,二次函数
,二次函数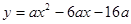 (
(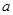 >0)的图像过点
>0)的图像过点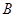 、
、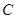 两点,点
两点,点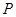 是线段
是线段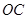 上由
上由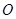 向
向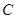 移动的动点,线段
移动的动点,线段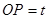 (1<
(1<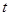 <8)。
<8)。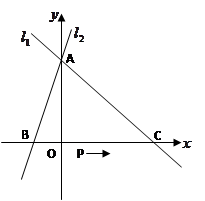
⑴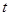 为何值时,
为何值时,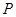 为圆心
为圆心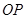 为半径的圆与
为半径的圆与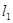 相切;
相切;
⑵设抛物线对称轴与直线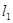 相交于点
相交于点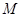 ,请在
,请在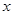 轴上求一点
轴上求一点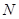 ,使
,使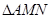 的周长最小;
的周长最小;
⑶设点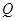 是
是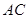 上由
上由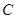 向
向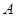 移动的一动点,且
移动的一动点,且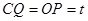 ,若
,若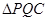 的面积为
的面积为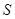 ,求
,求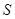 与
与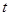 的函数关系式,当
的函数关系式,当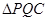 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出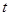 的值。
的值。
相关知识点
推荐套卷
如图,直线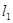 交直线
交直线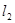 于
于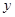 轴上一点
轴上一点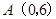 ,交
,交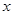 轴上另一点
轴上另一点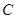 ,
,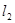 交
交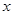 轴于另一点
轴于另一点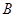 ,二次函数
,二次函数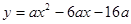 (
(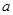 >0)的图像过点
>0)的图像过点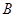 、
、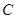 两点,点
两点,点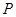 是线段
是线段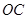 上由
上由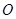 向
向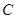 移动的动点,线段
移动的动点,线段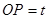 (1<
(1<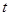 <8)。
<8)。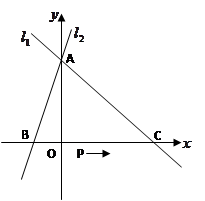
⑴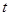 为何值时,
为何值时,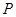 为圆心
为圆心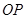 为半径的圆与
为半径的圆与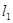 相切;
相切;
⑵设抛物线对称轴与直线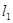 相交于点
相交于点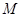 ,请在
,请在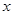 轴上求一点
轴上求一点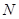 ,使
,使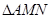 的周长最小;
的周长最小;
⑶设点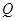 是
是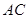 上由
上由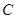 向
向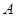 移动的一动点,且
移动的一动点,且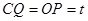 ,若
,若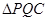 的面积为
的面积为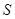 ,求
,求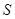 与
与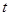 的函数关系式,当
的函数关系式,当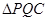 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出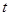 的值。
的值。