如图,在平面直角坐标系中,O为坐标原点,已知A(2, ),C(4,0),E点从O出发,以每秒1个单位的速度,沿边OC向C点运动,P点从O点出发,以每秒2个单位的速度,沿边OA与边AC向C运动,E、P两点同时出发,设运动时间为t秒。
),C(4,0),E点从O出发,以每秒1个单位的速度,沿边OC向C点运动,P点从O点出发,以每秒2个单位的速度,沿边OA与边AC向C运动,E、P两点同时出发,设运动时间为t秒。
(1) 求∠AOC的度数,
(2) 过 E作EH⊥AC于H,当t为何值时,△EPH是等边三角形。
(3)设四边形OEHP的面积S,求S关于t的函数表达式,并求出其最大值。
(4)当△OPE与以E、H、P为顶点的三角形相似,求P点坐标。
相关知识点
推荐套卷




 的图像与直线AB相交于C、D两点,若
的图像与直线AB相交于C、D两点,若 ,求k的值。
,求k的值。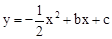 经过C、B两点,与x轴的另一交点为D。
经过C、B两点,与x轴的另一交点为D。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号