给出下列四个命题:
①若 三边为
三边为 ,面积为
,面积为 ,内切圆的半径
,内切圆的半径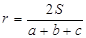 ,则
,则
由类比推理知四面体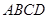 的内切球半径
的内切球半径
(其中, 为四面体的体积,
为四面体的体积,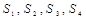 为四个面的面积);
为四个面的面积);
②若回归直线的斜率估计值是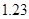 ,样本点的中心为
,样本点的中心为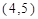 ,则回归直线方程是
,则回归直线方程是 ;
;
③若偶函数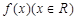 满足
满足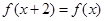 ,且
,且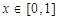 时,
时, ,则方程
,则方程 有3个根.
有3个根.
④若圆 ,圆
,圆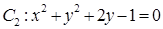 ,则这两个圆恰有4条公切线.
,则这两个圆恰有4条公切线.
其中,正确命题的序号是 .(把你认为正确命题的序号都填上)
推荐套卷
给出下列四个命题:
①若 三边为
三边为 ,面积为
,面积为 ,内切圆的半径
,内切圆的半径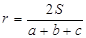 ,则
,则
由类比推理知四面体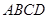 的内切球半径
的内切球半径
(其中, 为四面体的体积,
为四面体的体积,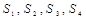 为四个面的面积);
为四个面的面积);
②若回归直线的斜率估计值是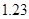 ,样本点的中心为
,样本点的中心为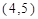 ,则回归直线方程是
,则回归直线方程是 ;
;
③若偶函数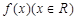 满足
满足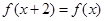 ,且
,且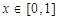 时,
时, ,则方程
,则方程 有3个根.
有3个根.
④若圆 ,圆
,圆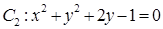 ,则这两个圆恰有4条公切线.
,则这两个圆恰有4条公切线.
其中,正确命题的序号是 .(把你认为正确命题的序号都填上)