如图，矩形ABCD在平面直角坐标系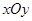
中，BC边在x轴上，点A(－1，2)，点C(3，0) ．动点P从点A出发，以每秒1个单位的速度沿AD向点D运动，到达点D后停止．把BP的中点M绕点P逆时针旋转90°到点N，连接PN，DN．设P的运动时间为t秒．经过1秒后，求出点N的坐标；
当t为何值时，△PND的面积最大？并求出这个最大值
求在整个过程中，点N运动的路程是多少？
相关试题
以下正确的是（）
，
、
时，一次函数的函数值y满足
，则一次函数的解析式为
或
和
相交于x轴上一点，则
的值是
的图像上有两点A（a、3）和B（3、b），则
的值（）
；
．
相关知识点
推荐套卷
如图，矩形ABCD在平面直角坐标系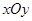中，BC边在x轴上，点A(－1，2)，点C(3，0) ．动点P从点A出发，以每秒1个单位的速度沿AD向点D运动，到达点D后停止．把BP的中点M绕点P逆时针旋转90°到点N，连接PN，DN．设P的运动时间为t秒．经过1秒后，求出点N的坐标；
当t为何值时，△PND的面积最大？并求出这个最大值
求在整个过程中，点N运动的路程是多少？
粤公网安备 44130202000953号