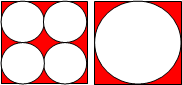
如图：两个正方形的边长均为2a，左边正方形内四个半径为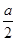
的圆依次相切，右边正方形内有一个半径为a的内切圆，在这两个图形上各随机撒一粒黄豆，落在阴影内的概率分别为
,
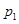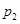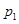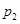,则,的大小关系是：（ ）
| A．= |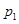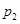
B．> |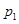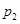
C．< |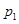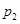
D．无法比较 |
，则a，b，c的大小关系是
满足
，则
的解是
的夹角为
，且
，在
ABC中，
，D为BC的中点，则
在
处连续，则
为等差数列
的前
项和，且
则
相关知识点
推荐套卷
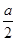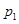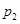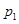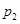如图：两个正方形的边长均为2a，左边正方形内四个半径为的圆依次相切，右边正方形内有一个半径为a的内切圆，在这两个图形上各随机撒一粒黄豆，落在阴影内的概率分别为,,则,的大小关系是：（ ）
| A．= |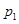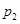
B．> |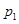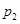
C．< |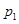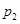
D．无法比较 |
粤公网安备 44130202000953号