如图,A、B两个转盘均被平均分成三个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.小敏分别转动两个转盘, 当两个转盘停止后,小敏把A转盘指针所指区域内的数字记为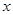 ,B转盘指针所指区域内的数字记为
,B转盘指针所指区域内的数字记为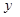 .这样就确定了点P的坐标
.这样就确定了点P的坐标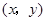 .(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.
.(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.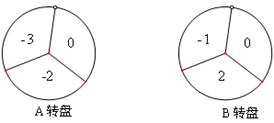
相关知识点
推荐套卷
如图,A、B两个转盘均被平均分成三个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.小敏分别转动两个转盘, 当两个转盘停止后,小敏把A转盘指针所指区域内的数字记为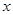 ,B转盘指针所指区域内的数字记为
,B转盘指针所指区域内的数字记为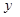 .这样就确定了点P的坐标
.这样就确定了点P的坐标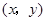 .(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.
.(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.