如图，直角坐标系中，以点A（1，0）为圆心画圆，点M（4，4）在⊙A上，直线y=－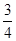
x+b过点M，分别交x轴、y轴于B、C两点．求⊙A的半径和b的值；
判断直线BC与⊙A的位置关系，并说明理由；
若点P在⊙A上，点Q是y轴上C点下方的一点，当△PQM为等腰直角三角形时，请直接写出满足条件的点Q（0，k）（k为整数）坐标．
相关试题
,则
___.
,当
时, 
随
的增大而增大,则关
的解的情况是.
,那么
可化简为.
的积为有理数____ ____．
相关知识点
推荐套卷
如图，直角坐标系中，以点A（1，0）为圆心画圆，点M（4，4）在⊙A上，直线y=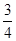－x+b过点M，分别交x轴、y轴于B、C两点．求⊙A的半径和b的值；
判断直线BC与⊙A的位置关系，并说明理由；
若点P在⊙A上，点Q是y轴上C点下方的一点，当△PQM为等腰直角三角形时，请直接写出满足条件的点Q（0，k）（k为整数）坐标．
粤公网安备 44130202000953号