在Rt△ABC中,∠ACB=90°,tan∠BAC=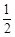 . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.若过点D作DE⊥AB于E,连结CF、EF、CE,如图1. 设
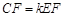 ,
,
则k = ;若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示. 求证:BE-DE=2CF;
若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.

相关知识点
推荐套卷

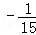 ,b=10.
,b=10. ;
; =3.
=3. 粤公网安备 44130202000953号
粤公网安备 44130202000953号