“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书券.写出转动一次转盘获得45元购书券的概率;
转转盘和直接获得购书券,你认为哪种方式对读者更合算?请说明理由.

相关知识点
推荐套卷
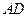 ∥
∥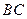 ,坝高10m,迎水坡面
,坝高10m,迎水坡面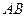 的坡度
的坡度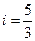 ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面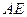 的坡度
的坡度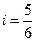 。
。
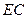 方向拓宽2.7m,求坝顶将会沿
方向拓宽2.7m,求坝顶将会沿
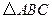 三个顶点的坐标分别为
三个顶点的坐标分别为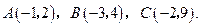
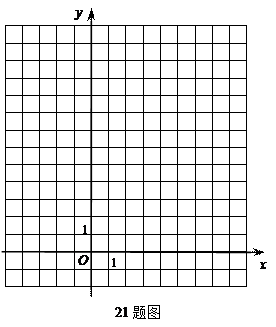
 所在直线的解析式。
所在直线的解析式。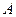 顺时针旋转
顺时针旋转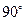 后得到的
后得到的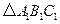 ,并求出
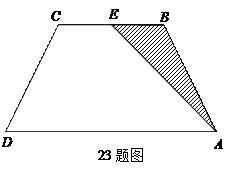
,并求出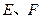 是平行四边形
是平行四边形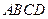 的对角线
的对角线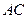 上的点,
上的点,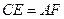 ,请你猜想:线段
,请你猜想:线段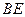 与线段
与线段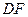 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。
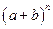 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应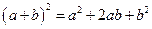 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着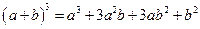 展开式中的系数等等。
展开式中的系数等等。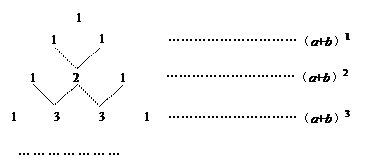
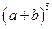 的展开式。
的展开式。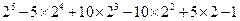
 粤公网安备 44130202000953号
粤公网安备 44130202000953号