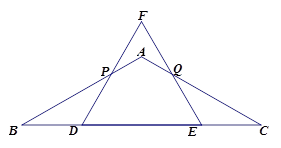
已知:在△ABC中,AB=AC,∠B=30°,BC=6,动点P以每秒 个单位从点B出发沿线段BA、AC运动,过点P作边长为3的等边△FDE,使得点D在线段BC上,点E在线段DC上.
个单位从点B出发沿线段BA、AC运动,过点P作边长为3的等边△FDE,使得点D在线段BC上,点E在线段DC上.如图(1),当EF经过点A时,动点P运动时间t为多少?
设点P运动t秒时,△ABC与△DEF重叠部分面积为S,求S关于t的函数关系式
如图(2),在点P的运动过程中,是否存在时间t,使得以点P为圆心,AP为半径的圆与△FDE三边所在的直线相切.如果存在,请直接写出t的值;如不存在,说明理由.

相关知识点
推荐套卷
 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.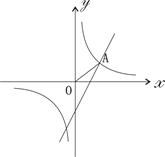

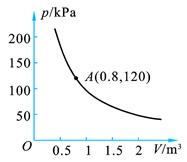
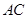 上的两点,且
上的两点,且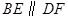 .
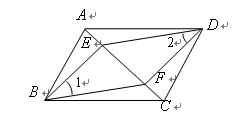
.
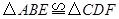 ;
;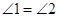 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号