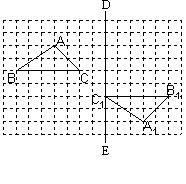
在如图的方格纸中,每个小正方形的边长都为l. (本小题满分6分)画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2;
要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转多少度?(直接写出答案)
在条件(2)中,计算△A2B2C2 计扫过的面积。
相关知识点
推荐套卷
在如图的方格纸中,每个小正方形的边长都为l. (本小题满分6分)画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2;
要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转多少度?(直接写出答案)
在条件(2)中,计算△A2B2C2 计扫过的面积。
