有3张扑克牌，分别是红桃3，红桃4和黑桃5，把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张，先后两次抽得的数字分别记为S和t，求
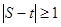的概率甲、乙两人做游戏，现有两种方案：A方案：若两次抽得相同花色则甲胜，否则乙胜，B方案：若两次抽得数字和为奇数则甲胜，否则乙胜；请问甲选择哪种方案胜率较高？
＋(－
)＋2
，325，-789，0，-23.13，0.618，-2004．相关知识点
推荐套卷
有3张扑克牌，分别是红桃3，红桃4和黑桃5，把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张，先后两次抽得的数字分别记为S和t，求
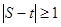的概率甲、乙两人做游戏，现有两种方案：A方案：若两次抽得相同花色则甲胜，否则乙胜，B方案：若两次抽得数字和为奇数则甲胜，否则乙胜；请问甲选择哪种方案胜率较高？
粤公网安备 44130202000953号