班主任让同学们为班会活动设计一个抽奖方案,拟使中奖概率为60%.小明的设计方案:在一个不透明的盒子中,放入10个球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 ▲ 个,白球应有 ▲ 个;
小兵的设计方案:在一个不透明的盒子中,放入4个黄球和1个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖.该设计方案是否符合老师的要求?试说明理由.
相关知识点
推荐套卷
 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.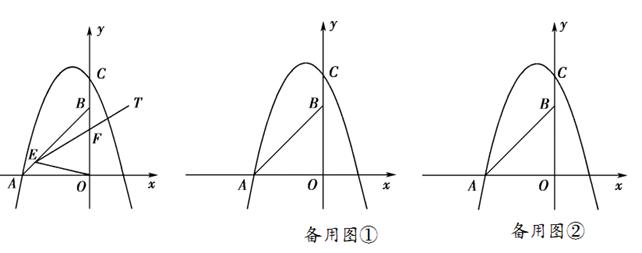
 ) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由. ,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.
,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.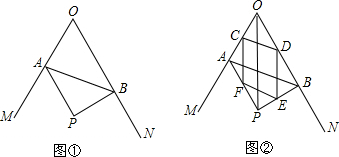

 粤公网安备 44130202000953号
粤公网安备 44130202000953号