已知二次函数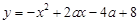
(1)求证:无论a为任何实数,二次函数的图象与x轴
总有两个交点.
(2)当x≥2时,函数值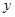 随
随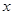 的增大而减小,求
的增大而减小,求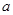 的取
的取
值范围.
(3)以二次函数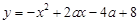 图象的顶点
图象的顶点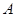 为一个顶点作该二次函数图象的内接正三角形
为一个顶点作该二次函数图象的内接正三角形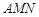 (M,N两点在二次函数的图象上),请问:△
(M,N两点在二次函数的图象上),请问:△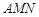 的面积是与a无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
的面积是与a无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
相关知识点
推荐套卷
已知二次函数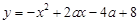
(1)求证:无论a为任何实数,二次函数的图象与x轴
总有两个交点.
(2)当x≥2时,函数值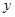 随
随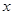 的增大而减小,求
的增大而减小,求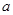 的取
的取
值范围.
(3)以二次函数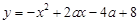 图象的顶点
图象的顶点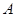 为一个顶点作该二次函数图象的内接正三角形
为一个顶点作该二次函数图象的内接正三角形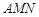 (M,N两点在二次函数的图象上),请问:△
(M,N两点在二次函数的图象上),请问:△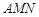 的面积是与a无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
的面积是与a无关的定值吗?若是,请求出这个定值;若不是,请说明理由.