已知抛物线 :
: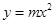 (
( ),焦点为
),焦点为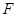 ,直线
,直线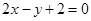 交抛物线
交抛物线 于
于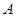 、
、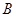 两点,
两点, 是线段
是线段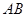 的中点,过
的中点,过 作
作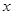 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点 ,
,
(1)若抛物线 上有一点
上有一点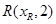 到焦点
到焦点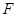 的距离为
的距离为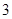 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使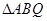 是以
是以 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出
的值;若不存在,说明理由。
推荐套卷
已知抛物线 :
: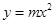 (
( ),焦点为
),焦点为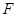 ,直线
,直线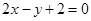 交抛物线
交抛物线 于
于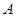 、
、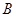 两点,
两点, 是线段
是线段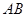 的中点,过
的中点,过 作
作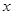 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点 ,
,
(1)若抛物线 上有一点
上有一点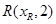 到焦点
到焦点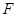 的距离为
的距离为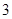 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使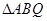 是以
是以 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出
的值;若不存在,说明理由。