已知一次函数y1 = 2x和二次函数y2 = x2 + 1。求证:函数y1、y2的图像都经过同一个定点;
求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
是否存在抛物线y3 = ax2 + bx + c,其图象经过点(
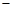 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
相关知识点
推荐套卷
已知一次函数y1 = 2x和二次函数y2 = x2 + 1。求证:函数y1、y2的图像都经过同一个定点;
求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
是否存在抛物线y3 = ax2 + bx + c,其图象经过点(
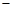 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。