甲、乙两名射击运动员,甲射击一次命中10环的概率为0.5,乙射击一次命中10环的概率为s,若他们独立的射击两次,设乙命中10环的次数为X,则EX=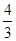 ,Y为甲与乙命中10环次数的差的绝对值.
,Y为甲与乙命中10环次数的差的绝对值.
求(1) s的值 (2) Y的分布列及期望.
相关知识点
推荐套卷
甲、乙两名射击运动员,甲射击一次命中10环的概率为0.5,乙射击一次命中10环的概率为s,若他们独立的射击两次,设乙命中10环的次数为X,则EX=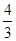 ,Y为甲与乙命中10环次数的差的绝对值.
,Y为甲与乙命中10环次数的差的绝对值.
求(1) s的值 (2) Y的分布列及期望.