如图，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上. (1)判断△ABC和△DEF是否相似，并说明理由.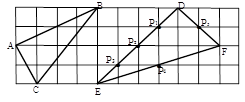
(2)P1、P2、P3、P4、P5、D、F是△DEF边上的7个格点，从这7个格点中选取三个点作为三角形的顶点，请写出两个与△ABC相似的三角形 、 .
，求方程ax2+bx+c=0的根。
相关知识点
推荐套卷
如图，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上. (1)判断△ABC和△DEF是否相似，并说明理由.
(2)P1、P2、P3、P4、P5、D、F是△DEF边上的7个格点，从这7个格点中选取三个点作为三角形的顶点，请写出两个与△ABC相似的三角形 、 .
粤公网安备 44130202000953号