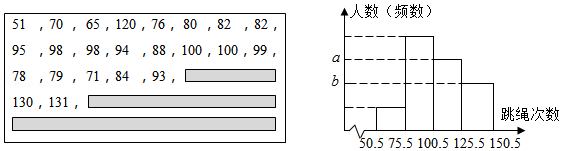
为了了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如图的频数直方图,图中的
,
满足关系式
.后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
(1)求问题中的总体和样本容量;
(2)求
,
的值(请写出必要的计算过程);
(3)如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数大约是多少人?(注:该年级共1000名学生)