如图所示,墙上挂有边长为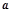 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为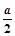 的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
A.1-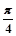 |
B.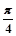 |
C.1-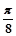 |
D.与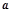 的取值有关 的取值有关 |
相关知识点
推荐套卷
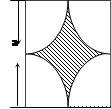
如图所示,墙上挂有边长为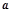 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为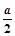 的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
A.1-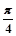 |
B.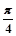 |
C.1-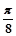 |
D.与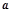 的取值有关 的取值有关 |
