已知:△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°.
问题1:如图1,若∠ACB=90°,AC=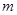 AB,BD=
AB,BD=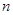 DC,
DC,
则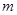 的值为_________,
的值为_________,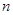 的值为__________.
的值为__________.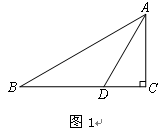
问题2:如图2,若∠ACB为钝角,且AB>AC,BD>DC.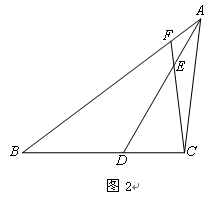
(1)求证: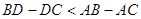 ;
;
(2)若点E在AD上,且DE=DB,延长CE交AB于点F,求∠BFC的度数.
相关知识点
推荐套卷
已知:△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°.
问题1:如图1,若∠ACB=90°,AC=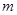 AB,BD=
AB,BD=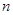 DC,
DC,
则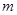 的值为_________,
的值为_________,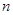 的值为__________.
的值为__________.
问题2:如图2,若∠ACB为钝角,且AB>AC,BD>DC.
(1)求证: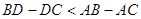 ;
;
(2)若点E在AD上,且DE=DB,延长CE交AB于点F,求∠BFC的度数.