已知各项均为非负整数的数列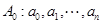
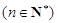 ,满足
,满足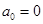 ,
, .若存在最小的正整数
.若存在最小的正整数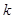 ,使得
,使得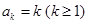 ,则可定义变换
,则可定义变换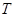 ,变换
,变换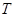 将数列
将数列 变为数列
变为数列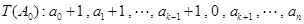 .设
.设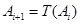 ,
,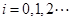 .
.
(Ⅰ)若数列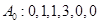 ,试写出数列
,试写出数列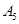 ;若数列
;若数列 ,试写出数列
,试写出数列 ;
;
(Ⅱ)证明存在唯一的数列 ,经过有限次
,经过有限次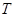 变换,可将数列
变换,可将数列 变为数列
变为数列 ;
;
(Ⅲ)若数列 ,经过有限次
,经过有限次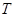 变换,可变为数列
变换,可变为数列 .设
.设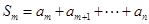 ,
,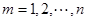 ,求证
,求证 ,其中
,其中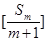 表示不超过
表示不超过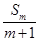 的最大整数.
的最大整数.
相关知识点
推荐套卷
已知各项均为非负整数的数列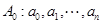
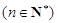 ,满足
,满足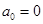 ,
, .若存在最小的正整数
.若存在最小的正整数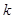 ,使得
,使得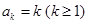 ,则可定义变换
,则可定义变换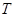 ,变换
,变换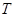 将数列
将数列 变为数列
变为数列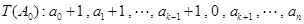 .设
.设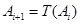 ,
,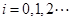 .
.
(Ⅰ)若数列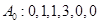 ,试写出数列
,试写出数列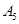 ;若数列
;若数列 ,试写出数列
,试写出数列 ;
;
(Ⅱ)证明存在唯一的数列 ,经过有限次
,经过有限次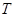 变换,可将数列
变换,可将数列 变为数列
变为数列 ;
;
(Ⅲ)若数列 ,经过有限次
,经过有限次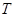 变换,可变为数列
变换,可变为数列 .设
.设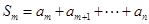 ,
,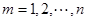 ,求证
,求证 ,其中
,其中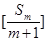 表示不超过
表示不超过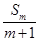 的最大整数.
的最大整数.