已知椭圆：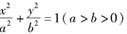
与X轴、y轴的正半轴分别交于A,B两点，原点O到直线AB的距离为
，该椭圆的离心率为
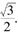
(I)求椭圆的方程；
(II)是否存在过点
的直线I与椭圆交于M,N两个不同的点，且对l外任意一点Q，有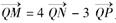
成立？若存在，求出l的方程；若不存在，说明理由.
、
两种型号的帐篷中选择一种，
顶，用不等式将题目中的不等关系表示出来．
取什么值时，一元二次不等式
对一切实数
都成立？推荐套卷
已知椭圆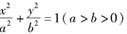：与X轴、y轴的正半轴分别交于A,B两点，原点O到直线AB的距离为，该椭圆的离心率为
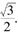
(I)求椭圆的方程；
(II)是否存在过点的直线I与椭圆交于M,N两个不同的点，且对l外任意一点Q，有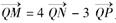成立？若存在，求出l的方程；若不存在，说明理由.
粤公网安备 44130202000953号