在平面直角坐标系
中，已知圆
和圆
.
（1）若直线
过点
，且被圆
截得的弦长为
，求直线
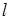的方程；
（2）在平面内是否存在一点
，使得过点有无穷多对互相垂直的直线
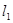和
，它们分别与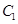圆
和圆相交，且直线
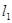被圆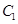截得的弦长的
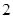倍与直线被圆截得的弦长相等？若存在，求出所有满足条件的点的坐标；若不存在，请说明理由.
相关试题
(
)的最大值与最小值；
(
是常数，且
)在区间
上有最大值
，最小值
，
.
的定义域；
的奇偶性，并说明理由；
定义域是
，当
时，
.
的解析式；
的值；（2）若
，求
，集合
.
，求实数
的取值范围； 
，求实数推荐套卷
在平面直角坐标系中，已知圆和圆.
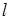（1）若直线过点，且被圆截得的弦长为，求直线的方程；
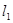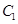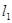（2）在平面内是否存在一点，使得过点有无穷多对互相垂直的直线和，它们分别与圆和圆相交，且直线被圆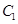截得的弦长的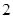倍与直线被圆截得的弦长相等？若存在，求出所有满足条件的点的坐标；若不存在，请说明理由.
粤公网安备 44130202000953号