图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.求证:PB与⊙O相切;
当PD=2
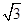 , ∠DPC=30°时,求⊙O的半径长.
, ∠DPC=30°时,求⊙O的半径长.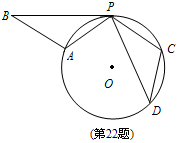
相关知识点
推荐套卷
图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.求证:PB与⊙O相切;
当PD=2
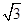 , ∠DPC=30°时,求⊙O的半径长.
, ∠DPC=30°时,求⊙O的半径长.