如图，现有一批设备需由抚州运往相距300千米的南昌，甲、乙两车分别以80千米/时和60千米/时的速度同时出发，甲车在距南昌130千米的A处发现有部分设备丢在B处, 立即以原速返回到B处取回设备，为了还能比乙车提前到达南昌，开始加速以100千米/时的速度向南昌前进，设AB的距离为a千米.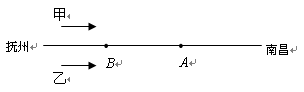
⑴写出甲车将设备从抚州运到南昌所经过的路程(用含a的代数式表示)；
⑵若甲车还能比乙车提前到达南昌,求a的取值范围.(不考虑其它因素)
相关试题
若二次函数的图象的对称轴是直线x=1.5，并且图象过A(0，－4)和B(4，0)
(1)求此二次函数的解析式；
(2)求此二次函数图象上点A关于对称轴对称的点A′的坐标.
cm.
的长(结果保留
).如图所示的曲线是一个反比例函数的图象的一支，且经过点P(1，3)．
（1）求该曲线所表示的函数的解析式；
（2）已知y≤2.5，直接利用函数图象，求自变量x的相应的取值范围．
sin60°－2sin45°相关知识点
推荐套卷
粤公网安备 44130202000953号