(本小题满分16分) [已知数列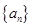
满足
,
.
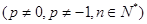(1)求数列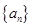的通项公式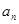
；
(2)若对每一个正整数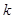
,若将
按从小到大的顺序排列后,此三项均能构成等
差数列, 且公差为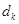
.①求
的值及对应的数列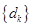
．
②记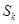
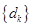为数列的前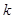项和，问是否存在
,使得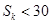
对任意正整数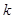恒成立?若存
在,求出的最大值；若不存在,请说明理由．
相关试题
中，四边形
是正方形，
平面
∥
与
所成角的余弦值；
平面
；
的正切值。
为圆心的圆与
轴交于点
，与
轴交于点
，其中
为坐标原点。
的面积为定值；
与圆
交于点
，若
，求圆
中，
是
的中点，点
是
的中点，将
分别沿
折起，使
两点重合于点
。求证：
时，求三棱锥
的体积。
的顶点
的坐标为
，
边上的中线所在直线方程为
的平分线所在直线方程为
，求
边所在直线的方程。
关于直线
对称,圆心
在第二象限,半径为
.
与圆
轴、
轴上的截距相等？若存在，求直线的方程；若不存在，说明理由。推荐套卷
(本小题满分16分) [已知数列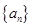满足,.
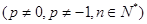(1)求数列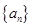的通项公式；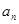
(2)若对每一个正整数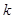,若将按从小到大的顺序排列后,此三项均能构成等
差数列, 且公差为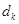.①求的值及对应的数列．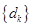
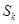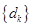②记为数列的前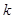项和，问是否存在,使得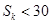对任意正整数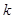恒成立?若存
在,求出的最大值；若不存在,请说明理由．
粤公网安备 44130202000953号